Event-Driven Consensus in the Age of Dynamic Availability

Designing a consensus protocol hinges on the assumptions one may make on the timing of the underlying network. If messages are guaranteed to arrive within a certain time, then the participants can safely move on if they haven’t heard from one of the participants within that time, assuming that they are faulty. If there is no such guarantee, the participants must use more clever strategies to come to agreement without knowing if a message was delayed or the participant is faulty.

In light of this, as protocol designers one of our first questions is whether we assume that all messages arrive within a certain message delay bound Δ, or if we are content with assuming that messages eventually reach their recipient. When we take the former approach, we assume synchrony, and when we take the latter approach, we assume asynchrony. Synchronous networks have the benefit that we can achieve consensus in a network with minority corruption deterministically ¹. On the other hand, asynchronous protocols require less than ¹⁄₃ corruption and must rely on randomization to ensure termination with high probability ^{2 3}. A key observation is that by assuming a conservative enough bound on the message delay, one could use a synchronous protocol in any network. In light of this, and given the drawbacks of asynchronous protocols, why do we care about asynchronous consensus protocols? Why not just assume that any network is synchronous (with a sufficiently large message delay assumption), and use a synchronous protocol?

The main drawback of assuming synchrony is that synchronous protocols rely on the (pessimistic) network delay assumption, even when the network conditions are better. Synchronous consensus protocols typically have the following construction: upon receiving a block proposal from the proposer, a party first sends the block to all of the parties in the network. At this point it starts a timer equal to the network delay assumption. If it has not heard of a conflicting block within this time, it knows that it can safely commit the block (i.e., that no other honest party will commit a conflicting block). This is because any honest party that received a conflicting block from the proposer will have heard of this block before their timer times out. Contrast this with the paradigm of asynchronous protocols. In asynchronous protocols, parties typically wait for a threshold number of messages of a certain type and immediately proceed to the next round of the protocol. In other words, asynchronous protocols are event driven rather than waiting for a timer to expire, and for this reason they are able to take advantage of improving network conditions. In an attempt to bridge the gap between the two, there has been a line of optimistically responsive protocols: these are protocols that rely on synchrony, but in the optimistic case (when certain additional constraints are met, e.g., a supermajority of honest parties), parties can commit faster.

Dynamic Availability

Let’s switch gears for a second and think about one of the most important advancements in consensus of the past two decades: dynamic availability. In the traditional permissioned setting, in which the set of parties participating in the protocol are fixed throughout the duration of the protocol, we can use the techniques of asynchronous protocols and optimistic responsiveness to achieve progress at the speed of the network. And what about the dynamically available setting, in which the set of parties participating in the protocol fluctuates, as in the Bitcoin protocol? Unfortunately, progress at the speed of the network is impossible in this setting ⁴. In short, this is because when a party doesn’t know the participation level of the network, it can’t be sure if it’s heard from sufficiently many parties to commit while maintaining safety.

Is that truly the end of it, then? Are dynamically available protocols inevitably bound to having parties wait for the pessimistic network delay in order to preserve safety? Or is it possible to achieve the best of both worlds: i.e., to be secure under the synchrony assumption yet commit in time that is closer to the actual network delay? This is the subject of the work “Low-Latency Dynamically Available Total Order Broadcast” ⁵. In this work, we answer this question in the affirmative. Our core contribution is the design of a dynamically available Total Order Broadcast (TOB) protocol, which eventually commits with a latency of O(Δ_ideal) in expectation for Δ_ideal < 2δ, where δ is the actual network delay. Note that TOB is basically the problem of keeping a shared list of events or transactions that everyone agrees on, even though the list is stored across many different computers — like what Bitcoin does.

Low-Latency Dynamically Available TOB

Our core idea is to run multiple instances of a dynamically available TOB protocol (such as ⁶), which takes a constant number of expected rounds for parties to commit a new block. Each instance is run based on one of k different assumptions on the upper bound on the network delay, denoted as Δ₁, …, Δ_i, Δ_i+1, …, Δ_k, where ∀iΔ_i+1 = 2Δ_i and Δ_k = Δ, i.e., the pessimistic network delay. This results in the creation of k logs. Observe that for all instances run with a delay greater than or equal to the actual network delay, the protocol maintains safety (honest parties won’t commit conflicting blocks in the same position in the log) due to the underlying TOB protocol. Allowing new blocks to be proposed in all instances simultaneously would lead to conflicting logs across the different instances. Thus, only one instance is ever allowed to propose new blocks at a time. Initially, this responsibility lies with the instance that has the smallest delay bound, Δ₁. When a block B proposed in a lower-delay instance (e.g., Δ_i) is confirmed in that instance, π_i, it is then passed to the next higher instance, π_i+1, for reconfirmation (i.e., to be added to the log of π_i+1). However, if the lower delay bound does not hold, the protocol may stop receiving new input blocks, or parties may produce inconsistent outputs in that instance. In such cases, the responsibility for proposing new blocks shifts to the next higher instance, and parties stop engaging in the failed instance and all lower instances.

Assuming that the parties never move past the lowest delay that holds, the result is that for all π_{i ≥ ideal}, the log of π_i extends the log of π_i+1.

The protocol returns all k logs and it has the property that if a client has a correct assumption on the network delay, they listen to a log that enables them to enjoy safety with all other clients that also have correct assumptions on the network delay.

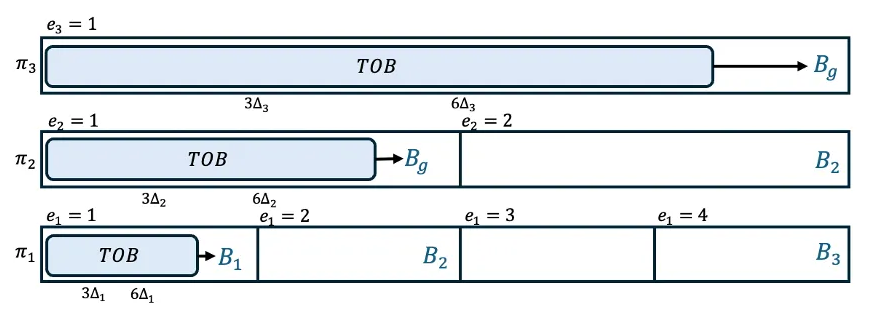
A depiction of an execution of the protocol with k = 3. The underlying TOB protocol proceeds in epochs. Each sub-protocol is executed with an increasing delay, where Δ_i = 2Δ_i−1. Because Δ₁ holds, new blocks are only decided in π₁ and blocks decided in π₁ may be used as input to π₂, and subsequently decided there. Similarly, blocks decided in π₂ may be used as input, and decided in, π₃. In epoch 3 of π₁, no block is decided due to a dishonest leader in that epoch of the TOB protocol.

The key idea for why this protocol achieves the desired latency is because parties commit a new block in protocol π_{j ≤ ideal} every constant number of rounds in expectation. In the higher protocols, those blocks are added to the logs as well. When a party commits one block, they commit all uncommitted blocks that it extends. Because Δ_i+1 = 2Δ_i ∀i ∈ [k], all logs for π_{j ≥ ideal} achieve an amortized latency of at least one block per O(1) timesteps of Δ_ideal. Note that this all assumes that parties never move past π_ideal.

Let’s go a step deeper and understand some of the key challenges that must be addressed to ensure the correctness of this protocol. As we just mentioned, to ensure that blocks are committed with a latency of O(Δ_ideal), the honest parties should never move to an instance past Δ_ideal. We must therefore address the following challenge:

• Honest parties should never propose new blocks in instances past π_ideal. This could cause inconsistent outputs in instance π_ideal, leading honest parties to believe that Δ_ideal < δ and attempting to move up to a higher instance.

On the other hand, to ensure liveness, we must ensure that if the parties are not making progress in protocols π_{j ≥ ideal}, they move to a higher instance.

• If the parties continue proposing new blocks in instances π_{j < ideal}, they should either make sufficient progress or move to higher instances.

Lastly, recall that we are in the dynamically available setting, meaning that honest parties may continue to join the protocol during the course of its execution. We must therefore also address the following challenge to ensure the liveness of the protocol:

• New parties joining the protocol have sufficient state to not stall the protocol. If the parties have detected that a given delay does not hold, and wish to move to a higher instance, new parties should not obstruct this.

To address the first challenge, we must ensure that the honest parties never see a false positive. That is, they should never detect that Δ_i for any i ≥ ideal does not hold. As mentioned before, the underlying TOB protocol ensures that for the instances corresponding to all delays that hold, the parties won’t create conflicting logs. What remains is to ensure that honest parties don’t see liveness violations for such delays. Why is this an obstacle? Parties only propose and vote for new blocks in a single instance (the one corresponding to their current belief of the lowest delay that holds). For all higher instances, they only propose and vote for blocks which were committed in lower instances already. So if a party proposes a new block in instance π_i, it will only be committed if all of the other parties also have the same estimate. We therefore ensure that parties update their estimates simultaneously using an additional protocol that acts as a beacon. Parties use this protocol to locally decide when to increase their estimate, with the guarantee that when one moves, they all move within a fixed amount of time. The beacon protocol is run with a delay of Δ, which is guaranteed to hold. The parties only start checking for progress in a given sub-protocol when they are sure that all parties have updated their estimates via the beacon protocol.

In addressing the second challenge, we seek to address the possibility that a subset of the honest parties may see evidence that a given Δ_j does not hold, while others do not. For example, it is possible for some honest parties to see progress in π_{j < ideal}, while other honest parties see no progress (this could happen if the delay does not hold and one party sees a much lower participation level than the other). Alternatively, an honest party might see two conflicting blocks decided in π_j, but given that the protocol has fluctuating participation, it may not be able to produce a proof to convince other honest parties that two conflicting blocks were certified. This can potentially ensure that parties are stuck on π_{j < ideal} and not making sufficient progress. To handle this challenge, we ensure that if the honest parties do not eventually converge on Δ_ideal, then this is because progress is being made at least at the speed of Δ_ideal, and consistent chains are being created in all π_{j ≥ ideal}. To achieve this, we have parties check that a block decided in π_j must be decided in π_j+1 sufficiently quickly (a.k.a. the time in which it should be decided if Δ_j holds — see the paper for details); otherwise this is evidence that Δ_j does not hold, and they attempt to increase their estimate.

Finally, we address the challenge with joining parties. In the dynamically available setting, new parties may continue to join the protocol as time goes on. The protocol relies on a beacon protocol to ensure that the parties move to a higher instance if they are not seeing progress. For our beacon protocol to work, it is necessary that all of the active honest parties want to move up when there isn’t progress. But when a new party joins the protocol, how do they know if sufficient progress hasn’t been made before they joined? To get around this, we have parties that wish to join the protocol detect if they should want to move up before they begin actively participating in the protocol, while they are in the recovering state. During recovery, a party learns the state of the logs for each instance as well as the time the parties entered the current instance. Using this information, the joining party can detect if sufficient progress has been made in the current sub-protocol. As a result, once a party becomes active in the protocol, its input to the beacon protocol reflects the progress that has been made even before it began participation, ensuring that joining parties do not prevent parties from moving up when needed.

This project serves as a first step in designing dynamically available protocols that achieve latency closer to the actual network delay. Looking ahead, we hope to start addressing the following challenges:

1. Running k protocols simultaneously puts a much larger load on the network. Are there ways to improve the scalability of the protocol?
   
2. In its current state, the protocol allows parties to move up to higher instances when they’ve detected that a given delay does not hold. But if network conditions improve, parties cannot move down to lower instances.

References